In the previous section we saw the basic details such as wavelength and frequency of sound waves. In this section we will see some more details.
We have learned about frequency in the previous section. It is the number of compressions or rarefactions occurring in unit time. Let us now plot a new type of graph. In this graph, we plot time along the x-axis and 'wave disturbance' along the y-axis. Let us see how we can plot it:
1. First we take up a position by the side of the path of the wave, ready with a stop watch.
2. Start the stop watch at the instant when a compression pass us.
3. In a compression, the air molecules are compressed to the maximum possible value. That means, it is a maximum disturbance.
4. So, at time equal to zero, plot this ' maximum disturbance value' on the y-axis. This is shown in the fig.5.6 below:
5. Now, the time is passing. With the passage of time, the disturbance at the point where we stand, becomes smaller and smaller. Note down these 'decreasing disturbance values' and the corresponding times.
6. After some time, the disturbance reaches the least possible value. It is a rarefaction.
7. After the rarefaction, the pressure begins to increase and reaches a compression. And the cycle continues with the passage of time.
8. Plot the disturbance values at corresponding times. When we join all those points, we will get a smooth curve.
9. This curve resembles the distance-pressure curve that we saw before. It is shown in the fig.5.6 above.
10. Such a 'time-wave disturbance' graph can be used to distiguish between sounds of different frequencies.
• Consider any time interval 't' for two different sounds.
♦ This 't' must be same for both the sounds. This is shown in the fig.5.7 below:
• Consider the 'number of maximum disturbances' n during this 't'
• For a sound of low frequency, n will be less
♦ We call a sound of low frequency as 'a low pitched sound'
• For a sound of high frequency, n will be more
♦ We call a sound of high frequency as 'a high pitched sound'
The next property that we have to learn is Amplitude. We have earlier seen how to fix up the position of the x-axis. It was explained using fig.5.3 at the beginning of the previous section. Let us recall:
1. First find the average of the following two:
• Maximum disturbance
• Minimum disturbance
2. Mark this average value on the y-axis. It will be exact midway between the maximum and minimum values
3. Draw the x-axis through this mark.
■ Now we can define amplitude:
• Amplitude is the magnitude of the maximum disturbance above the average value. It is marked as 'A' in the fig.5.8 below:
• It is also equal to the magnitude of the minimum disturbance below the average value.
■ Thus we can say that, a soft sound will have a low amplitude and a loud sound will have a high amplitude. This is shown in the fig.5.9 below:
• In the fig.5.9 above, the frequencies of the two sounds are the same. But the soft sound has a small amplitude, while the loud sound has a large amplitude.
• Sound can be created by striking a drum. When we strike a drum, we are doing a work.
• Part of this work causes the vibration of the membrane of the drum, and thus sound is produced.
• We can say that, part of the work is converted into sound energy. This energy travels as waves.
1. Consider a flow of sound energy through a tunnel. In the fig.5.10(a) below, flow of this energy is indicated by the red arrows.
2. Now consider fig.5.10(b). A square of side 1 m is placed at the mouth of the tunnel.
3. The side of the square is 1 m. So area of the square is 1 m2.
4. Let 'E' be the total amount of energy passing through this square in a time duration of 't' seconds.
5. Then the amount of energy passing through the square in 1 second = E⁄t.
This ' E⁄t ' is the intensity of the sound energy flowing through the tunnel.
■ So intensity of sound can be defined as:
The amount of sound energy passing through unit area per second is called intensity of sound.
• Let us find it's unit:
1. We know that energy per second is joules per second
2. One joule per second is 1 watt
3. So unit of the intensity of sound is watts/m2
■ We sometimes use the terms loudness and intensity interchangeably. But they are not the same.
Consider an example:
• Two sounds have the same intensity. But a person hear one of them more loudly. One of the many possible reasons is:
♦ There are some obstructions in the path of one sound, while there are no obstructions in the path of the other.
• The listener will hear the second with no obstructions more loudly
• So we can not use 'intensity' and 'loudness' interchangeably
Observe the graphical representation of a wave given in fig.5.11 below:
(i) What is the amplitude of the wave
(ii) What is the wave length
(iii) Calculate the frequency of the wave if it took 0.2 s to reach A
Solution:
Part (i): Amplitude of the wave is 2
Part (ii): Consider the first two crests. The distances corresponding to them are 2 m and 10 m. So the wave length, λ = 10 - 2 = 8 m
Part (iii):
■ We know that speed = distance⁄time = 24⁄0.2 = 120 m s-1.
■ Also we have, speed = wavelength × frequency
Given:
• Wave length, λ = 8 m
• Speed, v = 120 m s-1
• So frequency, ν = speed⁄wave length = 120⁄8 = 15 Hz
Solved example 5.5
Graphical representation of two waves of the same amplitude are given in fig.5.7 below:
(i) What are the wavelengths
(ii) What is the frequency of each wave if both of them travel 12 m in 0.25 s
Solution:
Part (i):
Wave in fig(a): Consider the first two crests. The distances corresponding to them are 1 m and 5 m. So the wave length, λ = 5 - 1 = 4 m
Wave in fig(b): Consider the first two crests. The distances corresponding to them are 0.5 m and 2.5 m. So the wave length, λ = 2.5 - 0.5 = 2.0 m
Part (ii):
■ Both the waves travel the same distance in same time. So their speeds are equal.
We know that speed = distance⁄time = 12⁄0.25 = 48 m s-1.
■ Also we have, speed = wavelength × frequency
Wave in fig(a):
Given:
• Wave length, λ = 4 m
• Speed, v = 48 m s-1
• So frequency, ν = speed⁄wave length = 48⁄4 = 12 Hz
Wave in fig(b):
Given:
• Wave length, λ = 2 m
• Speed, v = 48 m s-1
• So frequency, ν = speed⁄wave length = 48⁄2 = 24 Hz
In the next section, we will see reflection of sound.
We have learned about frequency in the previous section. It is the number of compressions or rarefactions occurring in unit time. Let us now plot a new type of graph. In this graph, we plot time along the x-axis and 'wave disturbance' along the y-axis. Let us see how we can plot it:
1. First we take up a position by the side of the path of the wave, ready with a stop watch.
2. Start the stop watch at the instant when a compression pass us.
3. In a compression, the air molecules are compressed to the maximum possible value. That means, it is a maximum disturbance.
4. So, at time equal to zero, plot this ' maximum disturbance value' on the y-axis. This is shown in the fig.5.6 below:
 |
| Fig.5.6 |
6. After some time, the disturbance reaches the least possible value. It is a rarefaction.
7. After the rarefaction, the pressure begins to increase and reaches a compression. And the cycle continues with the passage of time.
8. Plot the disturbance values at corresponding times. When we join all those points, we will get a smooth curve.
9. This curve resembles the distance-pressure curve that we saw before. It is shown in the fig.5.6 above.
10. Such a 'time-wave disturbance' graph can be used to distiguish between sounds of different frequencies.
• Consider any time interval 't' for two different sounds.
♦ This 't' must be same for both the sounds. This is shown in the fig.5.7 below:
 |
| Fig.5.7 |
• For a sound of low frequency, n will be less
♦ We call a sound of low frequency as 'a low pitched sound'
• For a sound of high frequency, n will be more
♦ We call a sound of high frequency as 'a high pitched sound'
1. First find the average of the following two:
• Maximum disturbance
• Minimum disturbance
2. Mark this average value on the y-axis. It will be exact midway between the maximum and minimum values
3. Draw the x-axis through this mark.
■ Now we can define amplitude:
• Amplitude is the magnitude of the maximum disturbance above the average value. It is marked as 'A' in the fig.5.8 below:
 |
| Fig.5.8 |
Next we will see loudness.
• If we hit a drum lightly, we will hear a soft sound. This is because, the light hit produces a light vibration. It does not produce much compression and rarefaction in the air. In other words, the disturbance produced is low. So the amplitude will be low.
• If we hit a drum hard, we will hear a loud sound. This is because, the hard hit produces a strong vibration. It produces a high compression and rarefaction in the air. In other words, the disturbance produced is high. So the amplitude will be high.■ Thus we can say that, a soft sound will have a low amplitude and a loud sound will have a high amplitude. This is shown in the fig.5.9 below:
 |
| Fig.5.9 |
Intensity of sound
• Sound is a form of energy. We have already learned about the Law of conservation of energy. (Details here).• Sound can be created by striking a drum. When we strike a drum, we are doing a work.
• Part of this work causes the vibration of the membrane of the drum, and thus sound is produced.
• We can say that, part of the work is converted into sound energy. This energy travels as waves.
1. Consider a flow of sound energy through a tunnel. In the fig.5.10(a) below, flow of this energy is indicated by the red arrows.
 |
| Fig.5.10 |
3. The side of the square is 1 m. So area of the square is 1 m2.
4. Let 'E' be the total amount of energy passing through this square in a time duration of 't' seconds.
5. Then the amount of energy passing through the square in 1 second = E⁄t.
This ' E⁄t ' is the intensity of the sound energy flowing through the tunnel.
■ So intensity of sound can be defined as:
The amount of sound energy passing through unit area per second is called intensity of sound.
• Let us find it's unit:
1. We know that energy per second is joules per second
2. One joule per second is 1 watt
3. So unit of the intensity of sound is watts/m2
■ We sometimes use the terms loudness and intensity interchangeably. But they are not the same.
Consider an example:
• Two sounds have the same intensity. But a person hear one of them more loudly. One of the many possible reasons is:
♦ There are some obstructions in the path of one sound, while there are no obstructions in the path of the other.
• The listener will hear the second with no obstructions more loudly
• So we can not use 'intensity' and 'loudness' interchangeably
Now we will see some more solved examples
Solved example 5.4Observe the graphical representation of a wave given in fig.5.11 below:
 |
| Fig.5.11 |
(ii) What is the wave length
(iii) Calculate the frequency of the wave if it took 0.2 s to reach A
Solution:
Part (i): Amplitude of the wave is 2
Part (ii): Consider the first two crests. The distances corresponding to them are 2 m and 10 m. So the wave length, λ = 10 - 2 = 8 m
Part (iii):
■ We know that speed = distance⁄time = 24⁄0.2 = 120 m s-1.
■ Also we have, speed = wavelength × frequency
Given:
• Wave length, λ = 8 m
• Speed, v = 120 m s-1
• So frequency, ν = speed⁄wave length = 120⁄8 = 15 Hz
Solved example 5.5
Graphical representation of two waves of the same amplitude are given in fig.5.7 below:
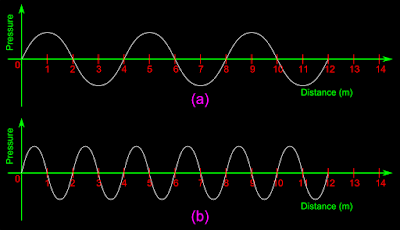 |
| Fig.5.12 |
(ii) What is the frequency of each wave if both of them travel 12 m in 0.25 s
Solution:
Part (i):
Wave in fig(a): Consider the first two crests. The distances corresponding to them are 1 m and 5 m. So the wave length, λ = 5 - 1 = 4 m
Wave in fig(b): Consider the first two crests. The distances corresponding to them are 0.5 m and 2.5 m. So the wave length, λ = 2.5 - 0.5 = 2.0 m
Part (ii):
■ Both the waves travel the same distance in same time. So their speeds are equal.
We know that speed = distance⁄time = 12⁄0.25 = 48 m s-1.
■ Also we have, speed = wavelength × frequency
Wave in fig(a):
Given:
• Wave length, λ = 4 m
• Speed, v = 48 m s-1
• So frequency, ν = speed⁄wave length = 48⁄4 = 12 Hz
Wave in fig(b):
Given:
• Wave length, λ = 2 m
• Speed, v = 48 m s-1
• So frequency, ν = speed⁄wave length = 48⁄2 = 24 Hz
In the next section, we will see reflection of sound.
No comments:
Post a Comment